수2 요 세 번째 경우에만 식이 성립하는데계산이 안되네요ㅜㅜ 도와주세요 X가 2 초과인
h(x) = 2x³-6x+1 라고 하면
h'(x) = 6x²-6 = 6(x-1)(x+1)이고
h(1) = -3, h(-1) = 5, h(2) = 5이므로
y = h(x)의 개형은
↗(1,5)↘(-1,-3)↗(2,5) 로 이어지고 이는 y = f(x)의 x≤2 부분의 개형입니다.
그리고 x>2부분의 개형은 a,b값에 따라 달라지는데
a의 부호에 따른 양음, 그리고 b의 값에 따른 축의 위치가 달라집니다.
일단 (2,9)에서 시작하는 선이 됩니다. (그 점 제외)
i) b≤2인 경우
a의 부호에 따라 x>2 부분 곡선은 단조 증가 혹은 단조 감소합니다.
i)-1 a<0 인 경우
g(t)값은 밑에서 부터 2,3,4,3,1,0 이 됩니다.
좌우극한함수값 합은
쭉 6이다가 k = -3에서 9가 되고,
쭉 12이다가 k = 5에서 8 되고,
쭉 3이다가 k = 9에서 1되고
그 후는 쭉 0입니다.
.... 조건 만족하는 경우네요.
아.... 두 자연수 a,b니까 a<0은 아예 불가능하네요. 제외합니다.
i)-2) a>0 이므로
g(t)값은 1, 2, 3, 2, 0, 1
인데 3이 쭉 지속되는 지점이 있습니다. -3<k<5일때인데
그때는 모두 9가 나오므로 하나만 나오지 않습니다.
ii) b>2인 경우
꼭지점 위치에 따라 g(t) 변화가 다릅니다.
꼭지점의 y좌표를 q라고 할때
q<-3이면 g(t)값은 1, 2, 3, ..... q<t<-3에서 모두 9가 나오므로 불가
q = -3이면 g(t)값은 1, 3, 5, 4, 2, 1 로 세 값의 합은 3, 9, 15, 11, 6, 4, 3으로 k = -3일때만 9가 됨.
-3<q<5이면 g(t)값은 1, 2, 3.........-3<t<q에서 모두 9가 나오므로 불가
q≥5 이면 -3<t<5에서 모두 9가 나오므로 불가
그러면 q = -3이어야 합니다. 꼭지점의 함수값이 -3이면 됩니다.
(그 외에는 안 됩니다.)
y = a(x-2)(x-b) + 9 는 x = (2+b)/2에 대칭이므로 저 식에 이 값을 대입한 결과가 -3이어야 합니다.
a((2+b)/2-2)((2+b)/2 - b) + 9 = -3
(a/4)(2+b-4)(2+b-2b) = -12
a(b-2)(2-b) = -48
a(b-2)² = 48
a,b는 자연수이고 b>2이므로 a,b-2가 자연수입니다.
48의 약수 중 제곱수는 1², 2², 4² 세 경우가 있고
b-2는 1, 2, 4일때이고
a는 48, 12, 3일때이고
b는 3, 4, 6 일때이므로
a+b값은 51, 16, 9가 되고
a+b의 최대값은 51이 됩니다.
-
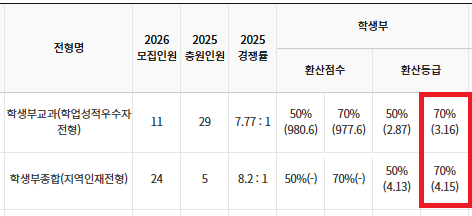
창원대 수시 .. 창원대를 목표로 하고 있는 09년생입니다 지금 제 내신이 5등급제 기준으로
2025.12.01 -
목포에서 롯데월드 가는 법 목포 버스 터미널에서 롯데월드로 갈 수 있는 경로 알려주세요
2025.12.01 -
애니?리뷰 유튜버 찾아주세요ㅠㅠ 무슨 검정머리 남자 캐릭터에 더빙하신분도 남자였던거같은데기승전결로 나눠서 기. 하고 설명하고
2025.12.01 -

발로란트 제한뜨는데 어떻게 해야하나요? 친구가 발로란트 한번해보자고 계정 빌려줬는데 제한이라고 접속이 안되는데 어떻게 해야하나요?
2025.12.01 -

KTX 12월31일 예매 수원이나 서울에서 부산으로 가는 열차를 예매하려고 하는데 언제 열리나요 오늘
2025.12.01 -

한국 지금 쉬었음청년40만명이라는데 4년대학졸업생이 많다던데요 쉬었음청년이 40만명인데 문제가 무엇인가요?
2025.12.01